< Deeplearning > Break up backpropagation

Let’s see a very simple handwriting formula derivation

Define

Firstly, let define some variables and operations

Gradient of the variable in layer L(last layer)

dWL = dLoss * aL

Gradient of the variable in layer L-1

dW(L-1) = dLoss * WL * dF(L-1) * a(L-1)

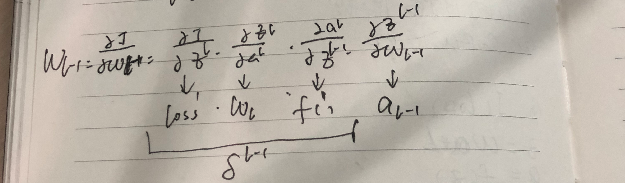
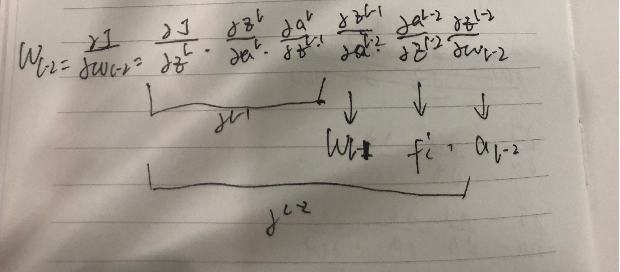
Gradient of the variable in layer L-2

dW(L-2) = dLoss * WL * dF(L-1) * a(L-1) * W(L-1) * dF(L-2) * a(L-2)

Summary

So, as we can see, the gradients of any trained variables only depends on the following three items:

• The trained variable itself.
• The derivative of the activation value from this layer.
• The activated value from the front layer.

Relations with gradient vanishing or exploding

The following cases may cause Gradient Exploding

• Training variables are larger than 1

• The derivative of activation function are larger than 1

• The the activated value are larger than 1.

The following cases may cause Gradient Vanishing

• Training variables are smaller than 1

• The derivative of activation function are smaller than 1,

• The the activated value are smaller than 1.

To prevent graident vanishing or exploding

From the view of training variables

To limit the trained variables into a proper range. We should use a proper variable initialization method, such as xavier initialization.

From the view of derivative of activation function

To limit derivative of activation function to a proper range, we should use non-saturated activation function such as Relu, instead of sigmoid

From the view of activated value

To limit the activation value in to proper range, we should use BatchNorm to make the activated value into a zero centered and variance to one.

From the view of model structure

To futher enhance the gradient to the deeper layer, we should use residual block to construct our network.